Many analog circuits can be calculated with simple algebra. This may involve an equation or a system of equations, but the calculations are quite simple. Take the differential amplifier, as an example. In a previous article, MasteringElectronicsDesign: Design a Differential Amplifier the Easy Way with Mathcad, I showed how to design the differential amplifier by solving a system of two equations with two unknowns using Mathcad. Since then, readers asked me if there is any other substitute for Mathcad that they can use to solve the system of equations. And the answer is, yes, there is one.
Microsoft Mathematics is a free application which is loaded with features. Besides its graphing, math formulas and units converter, it has an equation solver that can easily handle systems of equations. By changing a few values and letting the application calculate the unknowns, a user can tweak his circuit to match the design requirements.
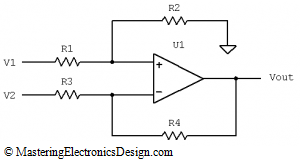
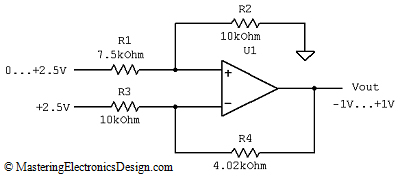
Let’s take the same example as in MasteringElectronicsDesign: Design a Differential Amplifier the Easy Way with Mathcad. In that article we designed a unipolar to bipolar converter using a differential amplifier (see Figure 1).
Figure 1
We wanted to calculate the resistors, so that an input of 0 to +2.5V (unipolar) would be converted into an output of -1V to +1V (bipolar).
To do this, we will use the differential amplifier transfer function, given by Equation (1).
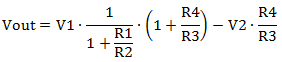 |
(1) |
(Note: The proof of this function can be found in my article MasteringElectronicsDesign:How to Derive the Differential Amplifier Transfer Function.)
Let’s choose V1 as the circuit input and V2 as a reference voltage that helps shift the output. For now, let’s consider Vref = 2.5V, a widely used voltage reference. The input signal span is 0 to +2.5V, so Equation (1) has two instances, as shown in Equations (2).
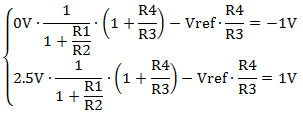 |
(2) |
If we choose two resistors, say R2 = R3 = 10 kohm, the other two, R1 and R4, can be calculated by solving system (2) with two unknowns, R1 and R4.
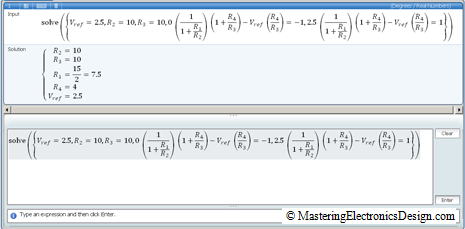
The system of equations (2) can be easily typed in Microsoft Mathematics. At the bottom of the worksheet just enter the following, in one line:
solve({V_ref=2.5, R_2=10, R_3=10,
0(1/(1+R_1/R_2))(1+R_4/R_3)-V_ref(R_4/R_3)=-1,
2.5(1/(1+R_1/R_2))(1+R_4/R_3)-V_ref(R_4/R_3)=1})
As you type, the application formats the system of equations as shown in Figure 2, lower area.
Figure 2
When you hit enter, Microsoft Mathematics solves the system and displays, in the upper area, the system of equations as it was entered, and the solution. Vref, R2 and R3 are included in the system so that one can play with those numbers, until an acceptable solution is found.
And this is it. The unipolar to bipolar converter is shown in Figure 3.
Figure 3
Microsoft Mathematics can be downloaded here: http://www.microsoft.com/en-us/download/details.aspx?id=15702





1 thought on “Design a Unipolar to Bipolar Converter the Easy Way with Microsoft Mathematics”