Design a Differential Amplifier with the Coefficients Identification Method
In the first part of this series, MasteringElectronicsDesign.com: Solving the Differential Amplifier – Part 1, I wrote that the common usage of the differential amplifier is as a gain circuit for the differential voltage at its inputs. When the circuit in Figure 1 has the resistor ratios equal
| (1) |
the amplifier transfer function is
| (2) |
and the circuit amplifies the difference between the input signals.
Figure 1
But the resistors’ calculation becomes a bit of a challenge, when one might be faced with designing a differential amplifier with a certain transfer function. The example I took in the first article was as follows: Given an input range of, -0.5V to 5.5V, the output has to swing between, -1.25V and +2.365V. I solved the problem by using the amplifier transfer function and a system of equations.
In this article I am going to write about designing the resistors of this differential amplifier using the method of coefficients identification.
Starting from the differential amplifier transfer function,
| (3) |
we note that this is a linear function Vo, with two variables: V1 and V2. However, if we consider one of these two variables a known value, say, V2, Vo becomes a simple linear function with one variable. Let’s note this function with Vo(V1).
The design requirements are as follows:
If Vin1 = -0.5V, then Vout1 = -1.25V and
If Vin2 = 5.5V, then Vout2 = 2.365V,
where by Vin1 and Vin2 I noted the input range limits, and by Vout1 and Vout2 I noted the output range limits.
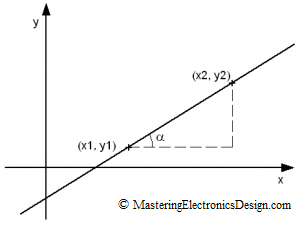
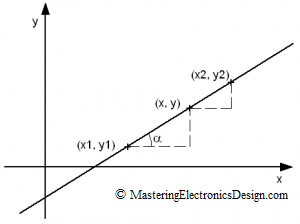
A linear function of first degree is a straight line which is determined by two points in the (x,y) plane (see Figure 2).
Figure 2
If we know one point (x1,y1) and the second point (x2,y2), we can determine the slope of the line, which is the tangent of the angle α between the x2-x1 and the hypotenuse of the triangle formed by the segments x2-x1 and y2-y1.
| (4) |
If we take an arbitrary point on this line between (x1,y1) and (x2,y2) and call it (x,y), the slope of the line has to be the same between the segment to the left and the one to the right of (x,y) point (see Figure 3).
| (5) |
Figure 3
Solving for y in equation (5), the result the well known linear function y(x), that we know it goes through the first point (x1,y1) and the second point (x2,y2).
| (6) |
Having said that, now we can compare the differential amplifier transfer function (3) with the linear function (6). When these two functions are identical, Vo(V1) is y(x) and V1 is the variable x. These are two linear functions that can be identical only if they have the coefficients identical, hence the name of the method.
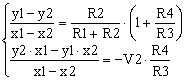 |
(7) |
As y(x) is determined by its two points in plan, so is Vo(V1). The given data points (Vin1, Vo1) and (Vin2, Vo2) determine the transfer function Vo(V1). Therefore, (7) can be rewritten as the following system of equations.
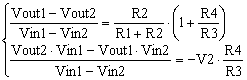 |
(8) |
After replacing the known values Vin1, Vin2, Vout1 and Vout2 and after calculations, the system becomes
 |
(9) |
which is exactly the result we had in part one of this series.
The system of equations (9) can be solved in the same manner as in the first article. In brief, we choose the voltage reference V2, based on the available voltage references we have in the system, then we calculate the ratio . Knowing this ratio we can calculate. Then, knowing the resistor ratios, by choosing a pair of resistors say, R1 and R3 we can calculate R2 and R4.
Therefore, if we choose V2 = 2.5V, R3 = 10 kOhm, and R1 = 10 kOhm, the result is R4 = 3.795 kOhm, or a standard value of 3.83 kOhm, with 1% tolerance. Also, R2 = 7.754 kOhm, or a standard value of 7.68 kOhm, with 1% tolerance.



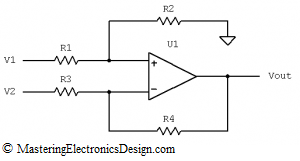


If your OpAmp has a bipolar source (+/- 12 V as an example) you can connect the AC source directly to V1 V2 inputs. Make R4/R3 = R2/R1 and equal with the gain you need. Chances are your source does not float and has a ground connection. Connect its output at V1 and connect R3 to ground. This is a classic way to design a non-inverting amplifier with the gain less than 1. Otherwise, if your gain is greater than 1, you can eliminate R1 and R2, connect the output of your source to the non-inverting input of U1 and connect R3 to ground. The gain will be 1+R4/R3.
thank you very much for explaining the differential amplifier. i have a question: i need to connect between v1 and v2 a AC source. is there a easy way to find the resistors for a given output range?
In this case you need to bias the input so that the output is somewhere in the middle of 0 to 5V. You did not mention what is the DC level at the OpAmp’s output, but let’s assume it has to be exactly in the middle, at 2.5V.
Connect the source at V1, connect R3 to ground and connect R2 to a DC level of 2.5V. If you decrease the input signal down to zero, you will see that the OpAmp output is 2.5V. As you increase the AC level, the output signal rides on top of 2.5V.
Choose R1, R2, R3, R4 so that R4/R1 = R2/R1 = 3, your gain.
no, i power the opamp 0 to 5V. the source is 0.5V peak to peak and i need the output to be 1.5V peak to peak.
Best you could make changes to the post name title MasteringElectronicsDesign.com : Solving the Differential Amplifier – Part 2 to something more specific for your blog post you create. I enjoyed the blog post nevertheless.
Well, it has a subtitle, “Design a Differential Amplifier with the Coefficients Identification Method”. However, it is part of a series of 3 articles, so I think the main title is appropriate.
Hi Adrian can you help me to solve an academic exercise which is very important for me. It involves thermocouple with differential amplifier. The question states that Vin=4.017 mOhm and Vout=1V, please calculate resistance for R1, R2, R3 and R4. Please help me !
I assume that the input voltage is Vin = 4.017 mV, not mOhm. For an academic exercise I would use the differential amplifier in this article, where R2/R1 = R4/R3 = gain. In this case the gain is the ratio between Vout and Vin which is 249. So, I would choose R1 = R3 = 100 ohm and R2 = R4 = 24.9 kohm, 1% tolerance.
For a practical application I would use an instrumentation amplifier, since the input signal is small and could be buried in noise. Or at least a low noise op amp.