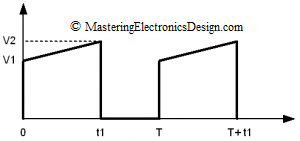
In a previous article, MasteringElectronicsDesign.com:How to Derive the RMS Value of A Trapezoidal Waveform – Part 1, I showed how to derive the RMS value of a trapezoidal signal with a flat plateau and different rise/fall time values. In some applications, the trapezoidal signal plateau is not flat, but rather a ramp, as shown in Figure 1. A typical example is a DC-DC converter, where the transformer winding current might look like the signal in Figure 1. Of course, in the DC-DC converter example, the amplitude is current and not voltage. No matter, the calculations are the same.
This waveform is still considered a trapezoidal waveform. Let’s calculate its RMS value.
The signal is linear between 0 and t1. Its expression as a function of time can be easily derived by first writing down the slope of the signal. Its slope is (V2-V1)/t1. Also, at origin, the signal value is V1. Therefore, by using simple algebra, the signal function is at follows:
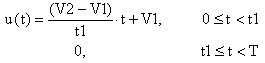 |
(1) |
For simplicity, let’s denote the slope with k = (V2-V1)/t1.
A periodic signal RMS definition is
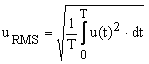 |
(2) |
and here is how to calculate the integral.
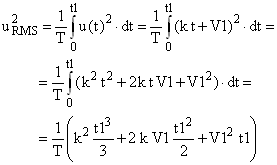 |
(3) |
Now let’s replace k with dV/t1, where dV is the difference V2-V1.
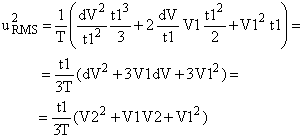 |
(4) |
Therefore the RMS value of the trapezoidal signal in Figure 1 is
| (5) |





Thank you, Adrian, just what I needed. Great website too. I’m impressed of your articles quality.
I’m glad you found it useful.
The slope on the waveform above V1 is positive; consequently u(t) looks stated incorrectly as:
u(t) = (V1-V2)/t1 *t +V1
should be u(t) = (V2-V1)/t1 *t + V1
The article howerever does indicate slope k positive as (V2-V1)/t1
Just wanted to note a minor inconsistency
Thank you Ed. Equation 1 shows now the correct slope.
thnks adrian
VERY GOOD document and easy to understand
How would you calculate the RMS value of an AC – Coupled Square wave under a load.
(basically a differentiator)
I thought it was:
VRMS = Vp * ?RC/(1+(?^2*R^2*C^2))
where:
? = 2?f (angular frequency)
C = ac coupled CAP value in Farads
R = Load in ohms
but the numbers don’t match my results under different “R” loads
You have a few question marks that most likely stand for characters that HTML did not understand. Write another post and replace characters like omega or pi with the word “omega” or “pi”, so that I could understand your equations.
Here is a quick method to calculate the RMS when a pulse goes through a capacitor C with a load R. The signal will spike up and then decay exponentially to zero with a time constant of tau = RC. Then repeats for the next pulse. Such a decaying function is
u(t) = Vp*exp(-t/tau), where tau is RC
Calculate this signal RMS by calculating the integral of u(t)^2. The result is
Vp*(-(1/2T)*tau*exp(-2*t/tau))^2, where Vp is the signal peak and T is the period.
Can we think of that trapezoidal wave from as off set trapezoidal waveform? If i find rms values of dc and trapezium (triangle + square of amplitude -v1 from time t2 to T) , there by calaculating resultant rms. Will I get the same result?? Tried Tried , almost tired to get the answer. plz help me out
I don’t have t2 in this figure, so tell me exactly at which figure you refer to. Or maybe it is a figure in The RMS Value of a Trapezoidal Waveform – Part 1? Let me know.
Adrian,
Minor edit – the “squared” symbol is missing in the second equation between equations 2 and 3.
Nice website!
Phil
Thank you for letting me know, Phil. I corrected it.
Hi Adrian,
Thanks for the awesome material, I have a question, I tried to split the shape into a small triangle on the top with a square wave on the bottom, so my equation is like this
(V2-V1)*sqrt(t1/3T) + V1*sqrt(t1/T)
but I can’t seem to get the same results as in equation(5), can you tell me what I did wrong?
Thanks
It does not work this way. You need to calculate it with the square root of the sum of squares and also the signals have to be uncorrelated. The waveform has to be split in time, not amplitude. Read this article MasteringElectronicsDesign.com: How to Calculate the RMS Value of an Arbitrary waveform.
thanks for such a good explanation