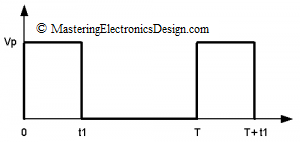
The RMS value of a pulse waveform can be easily calculated starting with the RMS definition. The pulse waveform is shown in Figure 1. The ratio t1/T is the pulse signal duty-cycle. As shown in other articles in this website (MasteringElectronicsDesign.com:How to Derive the RMS Value of a Trapezoidal Waveform and MasteringElectronicsDesign.com:How to Derive the RMS Value of a Triangle Waveform), the RMS definition is an integral over the signal period as in equation (1).
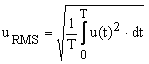 |
(1) |
The pulse function, with the variable “time”, is a constant, which is the signal amplitude, between 0 and t1 and zero from t1 to T as in (2).
| (2) |
where with u1(t) I noted the function of the waveform in Figure 1. After replacing u1(t) in equation (1) we can find the RMS value squared as in the following expression.
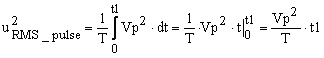 |
(3) |
Therefore, the RMS value of a pulse signal is
| (4) |
This expression can also be found as in (5)
| (5) |
where with D I noted the pulse signal duty cycle, D = t1/T.
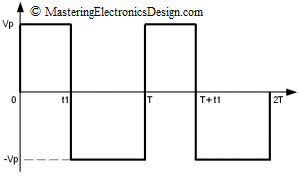
What if the pulse signal is bipolar, as in Figure 2?
Figure 2
In this case we should expect that the negative section of the signal to also contribute to the energy delivered to the load. To calculate its RMS value, let’s split the signal in two: from 0 to t1 and from t1 to T as in (6).
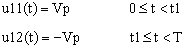 |
(6) |
where with u11(t) and u12(t) I noted the two sections of the waveform in Figure 2.
The RMS value of u11(t) is identical with the one shown in equation (3).
| (7) |
In a similar way, we can calculate the RMS value of u12(t):
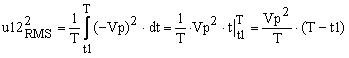 |
(8) |
The total RMS value of the bipolar pulse waveform is then calculated by applying the square root of the sum of squares of u11RMS and u12RMS.
| (9) |
After calculations, the RMS value of a bipolar pulse waveform is
| (10) |
As you can see, the bipolar pulse RMS value does not depend on its duty-cycle, and it is equal with its amplitude.
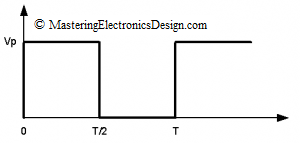
Knowing the RMS value of a pulse waveform we can easily calculate the RMS value of a periodic square signal. The square wave in Figure 3 is a pulse signal with 50% duty-cycle. Its RMS value can be calculated from equation (5), where D = 1/2. Its RMS value is given in (11).
Figure 3
| (11) |
>>> <<<





Hi,
I found this page very usefull for a recap but i belive there is a mistake in equation 7, which refers to equation 4, it should refer to equation 3.
At the moment it seems that the square of the Vp has vainish, to me it should be:
U11^2rms = Vp^2 * t1/T — or as per equation 3, U11^2= Vp^2/T * t1
Indeed, in eq 7 there was a typo. I corrected it. Thank you.
Hi,
Is this also valid for current pulse?
Yes, it is the same for current.
Yes it is valid for any function
Salut. Stii cumva cum as putea afla valoare medie a unui semnal dreptunghiular nesimetric dandu-se doar factorul de umplere si frecventa?
English translation: Hello. Do you know how can I find the average value of an asymmetric pulse signal, knowing just the duty-cycle and frequency?
You can think of it like this: A pulse signal with its amplitude between 0 and Vp (its peak value) and a duty-cycle d, has the average value:
VpulseAverage = d*Vp
If the signal is asymmetric, it has a negative value Vneg and a positive value Vpos. So, it’s amplitude is Vpos – Vneg and it is shifted down with Vneg. Therefore, the average value is:
VpulseAsymAverage = d * (Vpos-Vneg) + Vneg
where Vneg is taken with its negative sign.
Hi Adrian.
I have a question in relation to your post “Design a Bipolar to Unipolar Converter to Drive an ADC”.
I noticed that the feedback is configured to attenuate, and was wondering how does this affect stability, and phase margin. If I configure an inverting amp that attenuates in a similar manner will it be stable?
Also I can’t seem to launch an email from your web site. The verify for spam seems to be broken. Do you have an address I can send you a message?
Regards
Yes, it is stable, because it is a single pole system.
Thank you for telling me that the contact page does not work. I fixed it. Please send your message again.
How to solve it:
bipolar rectangular wave with 50% duty cycle and peak voltage of =-10v ?
I need more info. If it is a bipolar signal, I also need the positive peak voltage.
+-10V
Then your signal looks like the one in figure 2, with the difference that the duty cycle is 50%. The RMS value is given by equation 10.
Hey Adrian,
For the pulse in Figure 1, how do we find the AC rms value? I think I saw somewhere that the RMS^2=DC^2+ACrms^2 so ACrms^2=RMS^2-DC^2
What would be the DC component in figure 1? Is it Vp/2? If so, then ACrms^2=Vp^2*D-Vp^2/4
Let’s say D is 0.25, then ACrms=0 ??? Is this right?
How do you find ACrms is the above method is not correct?
“For the pulse in Figure 1, how do we find the AC rms value? I think I saw somewhere that the RMS^2=DC^2+ACrms^2 so ACrms^2=RMS^2-DC^2”
Yes, correct.
“What would be the DC component in figure 1? Is it Vp/2?”
No, it is the average value, which is Vp * D, or Vp * (t1/T).
Thank you very much! Now it makes a lot more sense!
If I have a bipolar dc pulse that produces +6 volts and +6 amps and -6 volts and -6 amps would peak power be 141 watts?
Frequency is 60Hz
Does not matter. Peak is independent of frequency.
If peak voltage is 6V and peak current is 6A, then peak power is 36 W for a pulse signal.
Hi, Having trouble wrapping my brain around how a bipolar pulse rms can be independent of duty cycle. How can a signal with lower duty cycle(less on time), deliver the same power as a signal with higher duty cycle(more on time)?
Actually, if it is a bipolar signal, there are no on/off states. The circuit that outputs the bipolar signal delivers power both during the time when the signal is positive as well as when it is negative. And RMS is a measure of power.
Mathematically, raising the signal to the power of two eliminates the negative sign. Indeed, the RMS value depends only on the signal absolute value. It is like bringing the signal negative side to the positive side.
If the signal is unipolar, then yes, you have an off time, when the signal caries no energy because it is zero, and so the RMS value depends on the duty-cycle as equation (5) shows.
I’m sorry, you’re right. Instead of fig2, I was thinking of a pulse, with the same peak and width, both on pos and neg pulses, but with an off time involved. Just to be clear, if a signal has an off time, regardless of shape, then the duty cycle would have to be involved in the rms value, correct?
If you have a bipolar signal that also has some zero time in its period, then yes, its RMS value will depend on the duty-cycle.
Hi. Can i ask how to find the formula for the Irms of a waveform wherein it is time dependent?
I don’t understand this question. A waveform is always time dependent. Mathematically, it is a function of time.
Hi,
I have a sequence of 8 pulses with 0.5 duty- cycle. A T is 25 mks . Vp=120 V Then 20 ms follow 0VDC . And again 8 pulses like previously. RMS calculation throughout 20.2 ms observation window is close to 0.85 V . Is it right ?
Your question is unclear. The 8 pulses repeat with a period T = 25 ms? Inside this 25 ms there is a 0 V amplitude with the duration of 20 ms? Or the 8 pulses have a duration of 25 ms, followed by 0 V with the duration of 20 ms?
Better send me a link that points to a figure.
I want to control a led that will turn on when duty cycle is above 50% and turn off when under 50%
i have a gate current of .01 and an anode voltage of +10 what would my rms voltage be?
I don’t understand your question. 0.01, what units? What is the circuit?
If this is correct, then the RMS of a full sinewave is equal to the RMS of a half square wave?
Yes. Both are Vp/sqrt(2).
Why? Therefore, this is a coincidence? Or it is about first harmonic of a half square wave is equal to a sinwave?
Because, physically, they both produce the same amount of power.
Hello, I have a bipolar rectangular wave with 20% Power Cycle. 10Vp (+-10V) 2KHz of frecuency and the multimeter indicates 8V, and with the same signal but 80% Power Cycle I got the same value of 8v, with 50% Power Cycle I got a value of 10V in the multimeter. Do you know why happens this?
I am going to assume that you set your multimeter on RMS measurement. It measures correctly when the duty-cycle is 50% and then errors out as the duty-cycle goes to extremes. Most likely this is due to multimeter’s insufficient bandwidth. Comments invited.
In my smps design do I have to convert my squarewave pulses to rms before substituting it to the Bmax formula? Since Bmax formula is in rms value of sinewave.
Yes, you do. The RMS current can be used in the formula regardless if the waveform is sine or square wave.
Hi Adrian, I’m trying to determine the DC equivalent of a current pulse. Based on some articles I read, I need to use the RMS value, which brought me to this post. Is the RMS appropriate for this situation since the value will be the same regardless of period for a given Ipk – if I have a 50A pulse at 50% duty cycle, the RMS will be the same whether the period is 1 second or 1us? Do you think for this situation, the average value is more appropriate? Thanks.
Hi Adrian,
I need to find the DC equivalent of a current pulse and based on some articles I read, it would be the RMS value. However, looking at the equation of RMS for a square wave, for a particular duty cylce say 50%, no matter what my period would be, the RMS will always be the same. For example, if I have a pulse of 100A, the RMS would be 70.7A whether the period is 1 sec. or 1 us. This doesn’t feel right because I would expect the DC equivalent for a 1sec period to be greater than a 1us period. What do you think? Is the average of the current pulse more appropriate? Thanks in advance for any input you can provide.
The period of 1 sec has an on time that’s much longer than a period of 1usec, but then it also has a longer off time, so it cancels out.
I am not sure what you are trying to say. The RMS value does not depend on time values, within reason. If you have a signal which is on for 3 days and then off for 3 days, then you can consider it as a DC signal depending on the corresponding processes in your system.
For example: You try to determine what connector you can choose, based on the RMS value of the current that has to go through one pin. If you have a PWM signal of say, 100 kHz, then yes, you can use the RMS value. But if you have a signal with a period of 10 seconds, then you have to look at the maximum value of the current over 10 seconds. That spec becomes now DC, not AC.