How to Calculate the RMS Value of an Arbitrary Waveform

Previous articles on MasteringElectronicsDesign.com talked about how to calculate the RMS of simple signals like a sine wave, trapezoidal and triangle signals, pulse and square signals. But, what about an arbitrary waveform? How do we calculate its RMS? Starting with the definition, as shown in previous articles, applying the integral, might not be an easy task. We need a different method. Enters the square root of the sum of squares.

The RMS value based on the square root of the sum of squares

If we have a few signals going through the same heating element, each signal heats the element independently of the other signals. This is valid, as long as the signals can be considered uncorrelated, that is, independent one of each other. The formula can be written as follows:

(1)

where with RMS1, RMS2, RMS3, I noted the RMS value of each signal.

The support for this method can also be found in Parseval’s Theorem. This theorem says that the integral of the square of a function is equal with the integral of the squared components of its spectrum. This means that the total energy of a waveform can be found in the total energy of the waveform’s components. As each signal forming the arbitrary waveform can be decomposed in its spectrum components, all these components contribute to the total energy of the arbitrary waveform and the rms value is the square root of the sum of squares of each spectrum component.

This is very helpful in calculating the RMS value of a periodic, arbitrary shaped signal. All we have to do is to divide that signal in slices which have a known shape, with a known RMS.

To show this method, let’s take a signal with a somewhat complicated shape, but known RMS value, and apply this method. Let’s consider the trapezoidal signal. I calculated the RMS value of a trapezoidal signal in this article, MasteringElectronicsDesign.com: How to Derive the RMS Value of a Trapezoidal Waveform – Part 1.

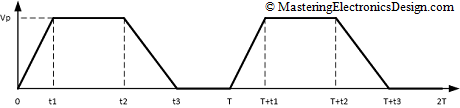
The trapezoidal signal is shown in Figure 1.

Figure 1

As shown in that article, the RMS value is

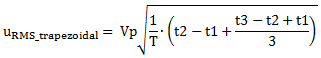(2)

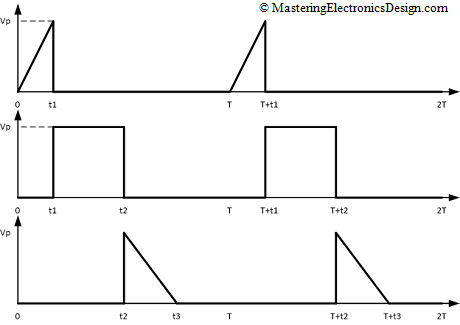
Let’s recalculate the trapezoidal signal RMS value with the method shown in Equation 1. We can divide the shape of the signal into two triangles (from 0 to t1 and from t2 to t3) and one pulse signal (from t1 to t2. This is depicted in Figure 2, where the three periodic signals are shown on three different graphs.

Figure 2

 Based on this article, MasteringElectronicsDesign.com: How to Derive the RMS Value of a Triangle Waveform, we can write the RMS value of the first triangle signal as

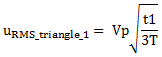(3)

 

where with u_{RMS_triangle_1} I noted the first signal RMS value, for the triangle between 0 and t1.
The third signal is also a triangle waveform and has the same RMS value. This is explained in MasteringElectronicsDesign.com: How to Derive the RMS Value of a Triangle Waveform as well. Therefore,

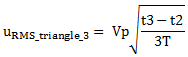(4)

where with u_{RMS_triangle_3} I noted the third signal RMS value, for the triangle between t3 and t2.
The second signal is a pulse waveform. Its RMS value is

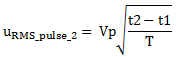(5)

where with u_{RMS_pulse_2} I noted the second signal RMS value, for the pulse between t1 and t2. This proof for a pulse RMS value is found in this article, MasteringElectronicsDesign.com: How to Derive the RMS Value of Pulse and Square Waveforms.

Now we can calculate the RMS value of the trapezoidal waveform be applying Equation 1.

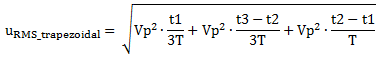(6)

which can be easily rewritten as follows,

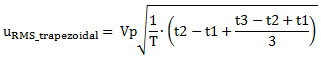(7)

exactly as in Equation 2.

Therefore, if you have a complex signal you can calculate its RMS value by splitting it in time, in known waveforms. In future articles I will use this method for other signals.