Norton’s Theorem is a powerful tool for solving electrical circuits. Like Thevenin’s Theorem, it simplifies the circuit one needs to study and dramatically reduces potential calculation errors.
Norton’s Theorem states that networks with voltage and current sources, as well as resistors are electrically equivalent to one single current source and one single resistor in parallel with the source. The theorem is valid for AC circuits, where instead of resistors there may be reactive components. Since this theorem sounds very much like Thevenin’s Theorem, one can only imagine that Norton’s current source is equivalent with Thevenin’s voltage source. Indeed, they are equivalent as we will see further.
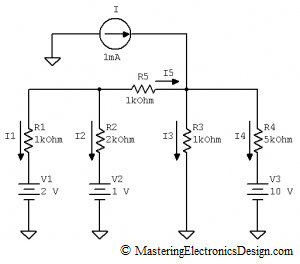
To demonstrate how powerful this theorem is, let’s take the same circuit we studied in How to Apply Thevenin’s Theorem – Part 1. This article describes how to apply Norton’s Theorem for a circuit with independent sources. Circuits with dependent sources have to be treated differently by Norton’s Theorem. We will see that in a future article.
Figure 1