Is there any link between a differential amplifier and a summing amplifier? Yes, it is. They can be easily converted one into the other one. While this article shows the conversion, the main purpose is to demonstrate how the same circuit can be viewed as a differential amplifier or as a summing amplifier, depending on the voltage levels in its inputs.
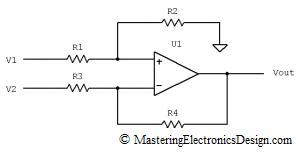
The differential amplifier is shown in Figure 1. It is mostly used to measure the voltage difference between its inputs. In addition, it can be used to achieve a linear function Vout(Vin) (Vout of Vin) where Vout is the voltage at the amplifier output, and Vin is the input voltage. In this case, any one of the inputs V1 or V2 can play the role of Vin. For details, read my articles Solving the Differential Amplifier Part 1, Part 2, and Part 3.
Figure 1
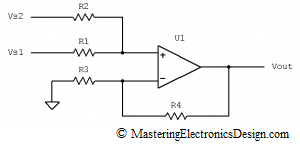
What is interesting about the differential amplifier, which I call a universal amplifier, is that it can be easily converted into a summing amplifier. In fact, they are one and the same circuit. In Figure 2 I drew the summing amplifier, where I noted the voltage levels at its inputs with Vs1 and Vs2. If you would like to read more about the summing amplifier go to this link: Solving the Summing Amplifier.
Figure 2
The differential amplifier can be seen as a summing amplifier, if we look at it differently. If, in Figure 1, we take R2 and move it on the left side of the OpAmp, as in Figure 2, without affecting its connections, the differential amplifier looks like a summing amplifier. The only difference is that, the differential amplifier sums V1 with a zero voltage, because R2 is connected to ground. Also, R3 is connected to V2 instead of being connected to ground.
Therefore, to convert the differential amplifier into a summing amplifier, all we have to do is to adjust the voltage levels as follows:
- Disconnect R2 from ground and connect it to Vs2,
- Connect R3 to ground.
Of course, these steps may be done backwards, if we need to convert a summing amplifier into a differential amplifier.
What about the transfer function of the summing amplifier? Can we easily derive it as well from a differential amplifier transfer function? Of course we can, and here is how.
The differential amplifier transfer function is shown in (1).
| (1) |
As I already said, the differential amplifier is a summing amplifier between V1 and zero volts, and with V2 = 0. Let’s rewrite the transfer function (1) as follows:
| (2) |
Why did I add 0V at V1 times the resistor ratios? Because, as I explained in The Differential Amplifier Transfer Function, any voltage on the non-inverting input multiplies the R4, R3 ratio plus one.
Now, if we connect R1 to Vs1 and connect R2 to Vs2, the transfer function becomes
| (3) |
where by k I noted the resistor ratio for Vs2. Using the Superposition Theorem, we realize that Vs2 “sees” a voltage divider made by R1 and R2, with the ratio of
| (4) |
For details on how to determine this ratio, read my article How to Derive the Summing Amplifier Transfer Function.
Replacing k in equation (3), we arrive at the summing amplifier transfer function as shown in equation (5).
| (5) |
Q. E. D.