What is the RMS value of a periodic signal? When a periodic signal is generated by a source connected to a load, a resistor for example, the RMS value is the continuous signal, the DC value which would deliver the same power to the load as the periodic signal.
This article shows how to derive the RMS value of triangle waveforms with different shapes and duty cycles.
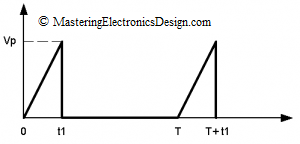
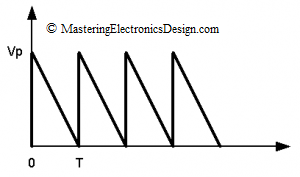
The triangle waveform in Figure 1 has a slower rise time than the fall time. In this case, the fall time is small so that it can be considered zero. If it is not zero, read further on deriving the RMS value of a triangle with comparable rise and fall times.
The RMS of this signal is calculated starting with the RMS definition, given in (1).
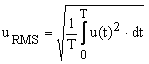 |
(1) |
The linear function from 0 to t1 has the following expression,
| (2) |
where with u1(t) I noted the linear function of the signal in Figure 1. This event is repeated every T period. After replacing (2) in equation (1), the RMS is
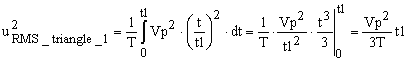 |
(3) |
or
| (4) |
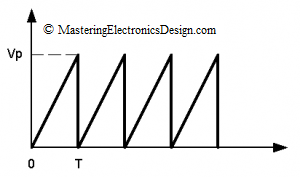
In equation (4) t1/T is the signal duty-cycle. If the triangle signal duty-cycle is 100%, as in Figure 2
then t1 = T and the RMS value becomes
| (5) |
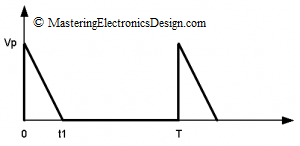
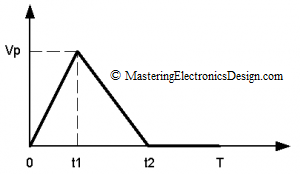
If we need to find the RMS value of a triangle with a fast rise time and slow fall time as in Figure 3
we can start from the same definition (1), taking into account that the linear function from 0 to t1 is as in equation (6).
| (6) |
After replacing (6) in (1), the RMS value is
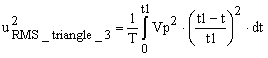 |
(7) |
Let’s change the variable to x = t1 – t. The integral becomes
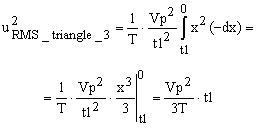 |
(8) |
Therefore, the triangle signal shown in Figure 3 has the same RMS value as the signal in Figure 1:
| (9) |
If the duty-cycle is 100%, as in Figure 4, then t1 = T and the RMS value is
| (10) |
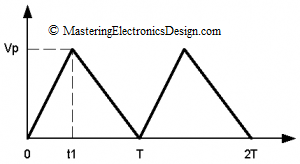
What if the triangle signal has the rise time and fall time comparable, as in Figure 5?
In this case we can calculate the RMS value by splitting the waveform in two: from 0 to t1 and from t1 to t2. The waveform expression in the time domain is given in (11),
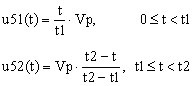 |
(11) |
where with u51(t) I noted the waveform section from 0 to t1, and with u52(t) I noted the section from t1 to t2.
We will use the square-root of sum of squares to calculate the RMS value of the waveform in Figure 5. The RMS value squared of u51(t) is already calculated in (3), and the result is
| (12) |
Also, the RMS value squared of u52(t) is calculated in (7) and (8) with the difference that (t1 – t) / t1 is replaced by (t2 – t) / (t2 – t1). The calculations are the same. The variable change is x = t2 – t. Therefore, the RMS value of u52 squared is
| (13) |
We can calculate now the RMS value of the triangle waveform in Figure 5, by applying the square root of the sum of squares.
| (14) |
The result is
| (15) |
If the duty-cycle is 100%, then t2 = T and the RMS value of the waveform in Figure 6 is
| (16) |
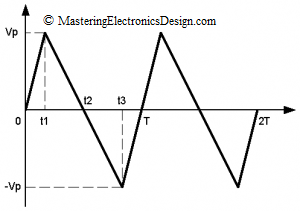
For a bipolar triangle, the waveform looks like the one in Figure 7.
We could calculate the RMS value by splitting the signal in 3, from 0 to t1, then from t1 to t3, and then from t3 to T. However, we already know the RMS value of the waveform from 0 to t2. It is given in equation (15). The RMS value of the waveform from t2 to T, is the same as the one from 0 to t2, with the difference that we need to replace t2 with T-t2, as in (17).
| (17) |
The reason is because it does not matter whether the signal is positive or negative, the power delivered to the load is the same. You can verify this statement by applying the integral as I did for the other waveforms and calculate the RMS value starting with its definition. Therefore, the RMS value of the bipolar triangle waveform is
| (18) |
and the result
| (19) |
>>> <<<





How do you calculate the RMS current through a resistor with a single triangular waveform. The waveform goes from 0A to 4A in 200 nanoseconds and the resistor is 75 ohms. Would be extremely greatful for help.
Thank you,
Bob
If you have just one single triangle pulse, then the RMS value goes from zero to its maximum value and then back to zero. The maximum value is given by equation (5) in this article, IRMSmax = Ip/sqrt(3), where Ip is the peak current, in this case 4A. So, during 400ns you will have a peak of 2.3Arms current. This is not very useful. Most of the time the RMS is calculated for a sustained periodic signal. More useful is the energy carried by this pulse, especially if this is an inrush current.
If this is an inrush current, the energy carried by this pulse is important. This is very helpful to see if the fuse you use will blow due to inrush current. The energy is called I^2*t. To calculate I^2*t, take equation (4) in which Vp becomes Ip, period T becomes variable t which is time, and t1 becomes tp (your pulse width). Therefore,
I^2*t = Ip^2 * tp * (1/3) = 4^2 * 400*10^(-9) * 0.33 = 2.13 *10^(-6) with units Amps^2*sec
The resistor value does not matter here.
I want formula for squared area of triangle.
The RMS value, in effect, is based on the power calculation of the triangle signal. The integral is the area of a periodic triangle signal. Equation 3 in this article is your answer.
Hi Sir,
How do we go about calculating the RMS for a changing current( based on a sine envelope) with constant TOn but of varying switching frequency?
Do I do a weighting of each individual RMS based on Ton/Line Period?
thanks!
I need to see the waveform to be able to answer this. Post a link to a graph on internet.
Last one (19) is wrong.
Right answer is Vp * 2 / sqrt(3)
You can see, the waveform is the same as in figure 7, but peak-to-peak is two times higher.
Mistake is in loosing sign. You are right there is no difference positive or negative signal is, but you are wrong when combining two of different signs there.
Sorry, my fault.
Vp / sqrt(3) is right, though
Please solve this triangular wave for dc Off set. how to calculate its RMS and average value.
What about the average value of the first one?
I am not sure what “first one” is. Please explain.
Awesome explanation. Few days before exam you have helped me write the RMS value so quickly.
How were you able to get the linear functions? Thank you.
You need to be specific. Which linear functions?
Please explain how equation 2 was obtained.
also, what does “t” represent in that equation. i.e equation 2
it is the expression of a liner function from basic algebra. Given two points in the plane x1,y1 and x2,y2, the linear function defined by these two points is
y(x) = (y2-y1)/(x2-x1)x + (x2y1-x1y2)/(x2-x1)
in our case x1 = 0, y1 = 0 because the function goes through zero. x2 = t1 and y2 = Vp. Replace in the above formula and you will find eq 2.
t is the variable time.
The last result is correct but confusing to the reader. A better comparison would be using waveforms of equal amplitude. Figure 6 has a peak-to-peak amplitude of Vp. Figure 7 has a peak-to-peak amplitude of 2*Vp. If the same Vp-p voltages are used for both, the equations are:
Figure 6: Vp/ROOT(3)
Figure 7: Vp/(2*ROOT(3))
Why this is important is that it illustrates the impact on RMS of adding a DC component to the waveform. There are many real-world systems that have sawtooth waveforms that maintain a constant peak-to-peak voltage/current but have varying DC components. The RMS value changes as a result.
Good post, Steve. Most likely, not confusing but a different way of looking at the graphs.
Hello Sir
Very nice post but please let me know how did you get equation (2). Also explain how to solve equation (5 2) for a graph with t1 and t2 to be equal to T/2 and T respectively.
Once again thank you for such a nice post
Good bye
1. It is the function of a straight line connecting to points on the graph: (0,0) and (t1,Vp). A quick look in a math textbook will show that the function is defined as f(x) = (y1-y0)/(x1-x0) * (x-x0) + y0, where (x0,y0) and (x1,y1) are the two points connected by the straight line and (x,y) is an arbitrary point on the line.
2. Just replace t1 and t2 with your values in equation 13.
hy adrian verry very explained article but …i tried 4,5 times for fig 3,U3 in eq (6) ..how u bring “t” ..and how to solve this ..plzzz..
ppllzz ..i will wait for ur reply
nadir.hpr@gmail.com
As I said in my previous posts, you use the function of a straight line that connects two points, as we learned in the basic algebra classes:
f(x) = ((y1-y0)/(x1-x0)) * (x-x0) + y0
In our case, u3(t) is the function and the variable is time. Replace y0 with Vp, x0 with 0, y1 with 0 and x1 with t1, as shown in the graph. The result is:
u3(t) = ((0-Vp)/(t1-0)) * (t-0) +Vp = -Vp * t/t1 + Vp = Vp * (t1-t)/t1
hi
please i’m seeking an answer to this one
in figure 5 how did we get that expression of vp.(t2-t)/(t2-t1)
and how we’re able to get one without an y intercept
It is the mathematical expression of a linear function that goes through 2 points:
– first point is the intersection of the function with the time axis at (t2, 0).
– second point is a random point (u52(t),t) between the apex and the intersection with the time axis, where with u52(t) I noted the value of the function at time t.