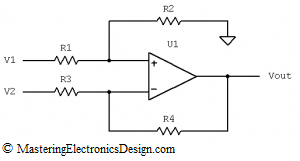
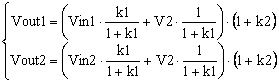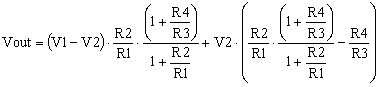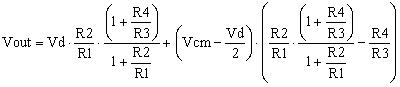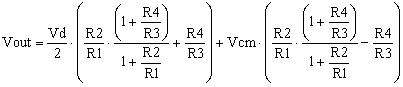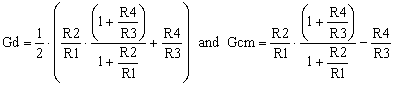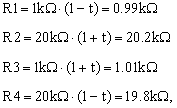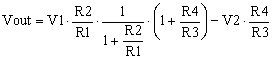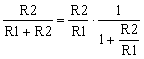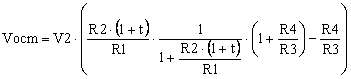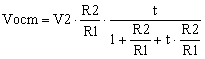Mastering Electronics Design – Page 9 – Electronics Design and Modeling with Emphasis on Analog Design

The Transfer Function of an Amplifier with a Bridge in the Negative Feedback

In allaboutcircuits.com forum an interesting circuit was posted. The question was, how to determine the transfer function, Vout/Vin?

The circuit schematic was drawn as in Figure 1.

Figure 1

To make a point regarding its feedback and for clarity, I redrew it as in Figure 2.

Figure 2

Now, things started to make more sense. R1 and R2 are feedback resistors. Also, the bridge does not alter the feedback, because there is no current going through it from Vout to the bridge and to U1 input. Assuming that U1 is close to an ideal amplifier, its bias current in the inverting input is zero. Therefore, whatever current emerges from the R1 and R2 node, noted with I12, and goes to the bridge is zero. Also, the current that goes into the inverting input, In, has to be zero.

It becomes clear now that the circuit is very simple. The only currents that Vin generates are local currents, I46 and I35, through the bridge legs.

Let’s write the voltage difference V46-V35, which is the voltage that alters Vout. I will call it Vbridge.

This voltage alters Vout because it appears in the amplifier input. For that reason, Vout is given by the following equation:

(1)

The amplifier output adjusts Vout so that V35 = 0V. The inverting input is at a virtual ground, so we can write Vbridge as

(2)

If we find out V46 as a function of Vin, the circuit is solved. How do we calculate it?

By inspecting the bridge we can write V46 as follows:

(3)

The current through R3 and R5 is I35 and its value can be written as in the following equation.

With I35 known we can calculate V3.

Following the same train of thoughts, V4 is

By replacing V3 and V4 in (3), V46 in (2) and Vbridge in (1), the transfer function is

Q.E.D. (quod erat demonstrandum)

>>> <<<

This equation shows us that, if the bridge is balanced, when

the output voltage is zero. Hence, this circuit can be used for tuning, or for measurements, when one of the resistors in the bridge is a sensor. Due to the resistor ratios in the transfer function, the actual resistor value does not matter. What matters is the ratio of these resistors. As a consequence, the circuit is insensitive to temperature variations because, if all resistors are from the same technological process, the voltage at output does not change with temperature. If we choose a good operational amplifier, with a low temperature drift and low offset, this amplifier can be used in precision measurements.

Converting a Differential Amplifier into a Summing Amplifier

by Adrian S. Nastase

Is there any link between a differential amplifier and a summing amplifier? Yes, it is. They can be easily converted one into the other one. While this article shows the conversion, the main purpose is to demonstrate how the same circuit can be viewed as a differential amplifier or as a summing amplifier, depending on the voltage levels in its inputs.

The differential amplifier is shown in Figure 1. It is mostly used to measure the voltage difference between its inputs. In addition, it can be used to achieve a linear function Vout(Vin) (Vout of Vin) where Vout is the voltage at the amplifier output, and Vin is the input voltage. In this case, any one of the inputs V1 or V2 can play the role of Vin. For details, read my articles Solving the Differential Amplifier Part 1, Part 2, and Part 3.

Figure 1

What is interesting about the differential amplifier, which I call a universal amplifier, is that it can be easily converted into a summing amplifier. In fact, they are one and the same circuit. In Figure 2 I drew the summing amplifier, where I noted the voltage levels at its inputs with Vs1 and Vs2. If you would like to read more about the summing amplifier go to this link: Solving the Summing Amplifier.

Figure 2

The differential amplifier can be seen as a summing amplifier, if we look at it differently. If, in Figure 1, we take R2 and move it on the left side of the OpAmp, as in Figure 2, without affecting its connections, the differential amplifier looks like a summing amplifier. The only difference is that, the differential amplifier sums V1 with a zero voltage, because R2 is connected to ground. Also, R3 is connected to V2 instead of being connected to ground.

Therefore, to convert the differential amplifier into a summing amplifier, all we have to do is to adjust the voltage levels as follows:

Disconnect R2 from ground and connect it to Vs2,
Connect R3 to ground.

Of course, these steps may be done backwards, if we need to convert a summing amplifier into a differential amplifier.

What about the transfer function of the summing amplifier? Can we easily derive it as well from a differential amplifier transfer function? Of course we can, and here is how.

The differential amplifier transfer function is shown in (1).

(1)

As I already said, the differential amplifier is a summing amplifier between V1 and zero volts, and with V2 = 0. Let’s rewrite the transfer function (1) as follows:

(2)

Why did I add 0V at V1 times the resistor ratios? Because, as I explained in The Differential Amplifier Transfer Function, any voltage on the non-inverting input multiplies the R4, R3 ratio plus one.

Now, if we connect R1 to Vs1 and connect R2 to Vs2, the transfer function becomes

(3)

where by k I noted the resistor ratio for Vs2. Using the Superposition Theorem, we realize that Vs2 “sees” a voltage divider made by R1 and R2, with the ratio of

(4)

For details on how to determine this ratio, read my article How to Derive the Summing Amplifier Transfer Function.

Replacing k in equation (3), we arrive at the summing amplifier transfer function as shown in equation (5).

(5)

Q. E. D.

Solving the Summing Amplifier

by Adrian S. Nastase

How to Design a Summing Amplifier Based on the Input and Output Voltage Level Requirements

In allaboutcircuits.com forum a member asked how can he drive a MOSFET that needs a voltage range of 4V to 5V with a DAC with the output range of 0V to 5V?

Initially I thought he should use a differential amplifier. However, based on the articles I published, MasteringElectronicsDesign.com: Solving the Differential Amplifier – Part 1, Part 2 and Part3 the solution based on a differential amplifier would require a negative voltage level in the input. Although V1 can be the input from 0V to 5V, V2 has to be negative, so that the output shifts to positive values.

Then I thought of the Summing Amplifier, or the Non-Inverting Summing Amplifier, which is shown in Figure 1. It is called a summing amplifier, because two signals are summed in one of the amplifier inputs. In this case, V1 and V2 are summed in the non-inverting input.

Figure 1

The summing of V1 and V2 is not direct. Resistors R1 and R2 make a weighted sum and this is what makes this amplifier very useful. As in the case with the differential amplifier, one can use this circuit to achieve any linear function. This article shows you how to design a summing amplifier based on the input and output requirements. You can also solve your amplifier with the calculator I posted here: MasteringElectronicsDesign.com: Summing Amplifier Calculator.

The transfer function of the summing amplifier is as follows.

(1)

You can find its demonstration in this article, MasteringElectronicsDesign.com: How to Derive the Summing Amplifier Transfer Function.

Let’s write down what we know:

If Vin1 = 0V then Vout1 = 4V and
If Vin2 = 5V then Vout2 = 5V,

where by Vin1 and Vin2 I noted the input range limits, and by Vout1 and Vout2 I noted the output range limits.

Let’s choose one of the summing amplifier inputs to be Vin, say V1.

Because we have two instances that we know, Vin1 and Vin2 and the corresponding outputs, Vout1 and Vout2, let’s rewrite equation (1) using these two instances.

(2)

This is a linear system of two equations with a lot of unknowns: R1, R2, R3, R4 and V2. However, we can simplify our life by grouping the resistors in ratios. The equations can be rewritten like this,

(3)

where by k1 and k2 I noted:

(4)

Now we are left with three unknowns, k1, k2, V2. I can simply consider V2 as a known value, because I can connect to R2 any voltage I want or, more conveniently, a voltage that I already have in the circuit. I will target for V2 = 5V, since there is already a DAC in this circuit with an output range of 0 to 5V. So I can assume there is a 5V reference in this circuit.

If k1 and k2 are the remaining unknowns, then (3) is a system of two equations and two unknowns as in (5), which can be easily solved.

(5)

It can be easily seen that the second equation becomes

(6)

so k2 has to be zero.

The result is k1 = 1/4 and k2 = 0.

This result shows that we do not need the resistors R3 and R4. Also, the ratio between R2 and R1 is 1/4. We can choose R2 = 1 kohm and a standard value for R1 = 4.02 kohm with a 1% tolerance.

The final circuit is shown in Figure 2.

Figure 2

Since k2 is zero, R3 is zero, configuring U1 as a repeater for the summed voltage in the non inverting input.

The Differential Amplifier Common-Mode Error – Part 2

by Adrian S. Nastase

Power Supply Output Current Measurement with a Differential Amplifier

When designing a differential amplifier, part of the art is to manage the errors affecting the precision of the circuit. In MasteringElectronicsDesign.com: The Differential Amplifier Common-Mode Error – Part 1 of this presentation I discussed the common-mode error of a differential amplifier. I also showed that, given the circuit in Figure 1, the common-mode voltage can be viewed as V2, when we consider V1-V2 as a signal that rides on top of V2. The same goes for V1, which can be considered the common-mode voltage of the differential amplifier when -(V1-V2) is the signal that rides on top of V1.

Figure 1

Most of the times, however, the input signals V1 and V2 would vary in time, whether there is an AC signal riding on top of a DC signal, or the input signals have a noise component as in Figure 2.

Figure 2

Because of that, it is customary to consider the common-mode voltage the average of the input signals, V1 and V2, as in Figure 3, so that the common-mode input signal lands in between V1 and V2.

Figure 3

Let’s note this signal with Vcm, and the difference V1-V2 with Vd.

(1)

From a signal difference point of view, each input will be referred to the common-mode voltage as shown in Figure 3. In this case, the difference signal Vd = (V1-V2) is split in two, so that the input R1 has a signal Vd/2 and the input R3 has a signal -Vd/2 as referred to the common-mode voltage Vcm.

What is the common-mode error in this case?

With these notations, I can express the input signals as in (2).

(2)

In MasteringElectronicsDesign.com: The Differential Amplifier Common-Mode Error – Part 1 I demonstrated that the output signal of the differential amplifier can be expressed as a function of V1-V2 and V2 as shown in (3).

(3)

By replacing V1 and V2 with the expressions (2), Vout becomes,

(4)

After calculations, the differential amplifier output becomes,

(5)

In equation (5), the first parenthesis is the differential gain and I will note it with Gd. The second parenthesis is the common-mode gain, noted with Gcm.

(6)

One can see that, if the resistor ratios are equal, Gcm is zero. We should note that this gain is the same as in the MasteringElectronicsDesign.com: The Differential Amplifier Common-Mode Error – Part 1, when the same expression multiplied V2. Indeed, this proves that, no matter the level of the common-mode voltage at the amplifier input, V2, Vcm or anything in between for that matter, the common-mode gain is the same.

Equation (5) also shows that the larger Vcm, the larger the common-mode error at the differential amplifier output. Since many times we cannot do anything about the common-mode voltage level, the electronics designer can only minimize the common-mode gain to reduce the error. This can be done by matching the resistor ratios.

One good example of using the differential amplifier is current measurement. One way is to measure the voltage drop across a small resistor. Another way is to measure the current inductively, with a magnetic probe.

Measuring the current through a network branch with a small resistor, called sense resistor, is preferred by many designers, because it can be very precise. Depending on the expected current level, the resistor value is chosen so that the voltage drop on this resistor is around a few hundred millivolts. A differential amplifier connected across the sense resistor amplifies the voltage drop to a manageable level, usually around 2.5V or 5V, so that an Analog to Digital Converter (ADC) can measure it with good resolution.

If the measurement has to be done at a power supply output (see Figure 4), the common mode voltage can be high, because it equals the power supply voltage level.

Figure 4

Let’s say that this is a 12V power supply that sources a nominal current of 5A to a system it powers. Based on the powered system functionality, the load current can vary in time and we need to monitor it. The voltage drop on Rsense has to be small enough so that the powered system still receives approximately 12V. If, instead of 12V, the system is powered at 11.9V, it can be good enough for most applications. Therefore, we can choose the drop on Rsense as 100mV. At 5A, the sense resistor has to be Rsense = 20 milliohms.

Also, let’s say we need to read the current with a microcontroller. For this, we need to use an ADC, with a reference voltage of 2.5V. We can design the differential amplifier resistors so that the nominal current of 5A means 2V at the amplifier output. This means that the nominal value is placed at 4/5^th of the ADC range, so that there is some room for positive or negative load current variation.

If the resistor ratios are equal, the differential gain, Gd is

(7)

The gain of the differential amplifier has to be

(8)

Let’s choose R2 = R4 = 20 kohms and R1 = R3 = 1 kohm. What tolerances should I select for these resistors? Resistors with 1% tolerance are quite common nowadays and they are not expensive. With 1% tolerance resistors, what is the common-mode error?

Since V2 = Vpower, let’s choose equation (3) to calculate the output voltage, for a nominal power supply current of 5A.

(9)

With the tolerance t = 0%, the output is the ideal nominal value Vout = 2V.

When the tolerance is t = 1%, and in the worst case in which the resistor values may be as follows,

(10)

the output voltage is Vout = 2.413V. The extra 0.413V is the common-mode error which is significant, as it represents 20.6% of the nominal value.

What if we use resistors with 0.1% tolerance? For the worst case scenario described above, the output becomes Vout = 2.042V. The error of 42mV means that the power source current is measured with an error of 2.1%. Depending on the application requirements, this measurement may be good enough, or may not be acceptable. If the error is too high, the designer has to choose either better matched resistors, or choose instrumentation amplifiers. Analog Devices’ AD620 can do the job with high precision.

There are some other questions that rise from this experiment:

Can the common-mode voltage damage the operational amplifier used for the differential amplifier circuit?

Is the sense resistor small enough so that the differential amplifier components do not modify its value and generate errors?

Is the offset voltage of the differential amplifier small enough so that the output offset does not appear as an error?

Are the operational amplifier input bias currents small enough, or their offset for that matter, so that there are no perceived errors at the amplifier output?

Is the temperature coefficient of the differential amplifier components small enough so that any temperature variation does not result in measurement errors?

I will discuss all these possible errors in future articles. Stay tuned.

The Differential Amplifier Common-Mode Error – Part 1

by Adrian S. Nastase

The common-mode voltage can bring errors in the differential amplifier applications. What is the common-mode voltage? The common-mode voltage is the voltage level common to both inverting and non-inverting inputs of the differential amplifier. In many applications, the differential amplifier is used to amplify the difference between two voltages, for later processing, or to isolate a signal from common-mode noise, or to amplify a signal that rides on top of some large voltage level. If the common-mode voltage is not rejected, it appears as an error at the amplifier output.

It is customary to consider the common-mode error as being negligible, based on the high Common-Mode Rejection Ratio (CMRR) of the operational amplifiers. This is not always the case. Once the electronics designer connects resistors around this amplifier, in a differential configuration, the common-mode error starts to be significant.

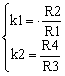
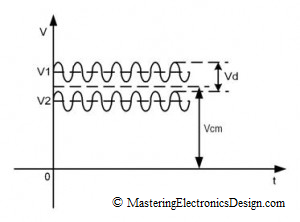
The common-mode voltage Vcm and the differential voltage Vd are shown in the group of equations (1).

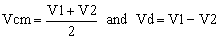(1)

Why these expressions? How was Vcm defined like that and why? We will start by looking at the significance of each input voltage in the differential amplifier.

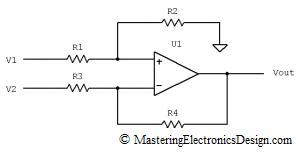
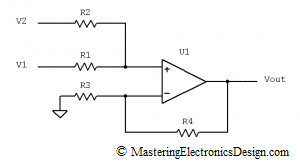
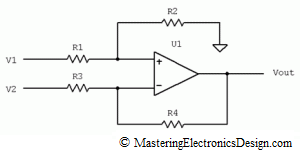
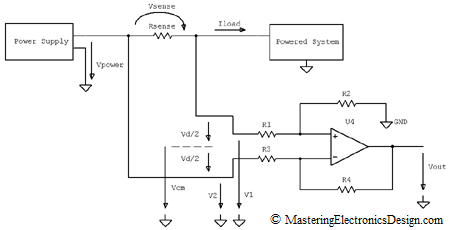
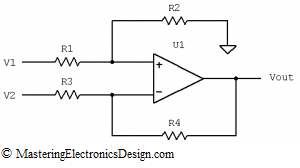
Looking at Figure 1, V1 is the input voltage between R1 and ground, while V2 is the input voltage between R3 and ground.

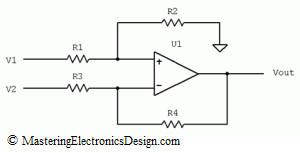
Figure 1

As we saw in MasteringElectronicsDesign.com: The Differential Amplifier Transfer Function, the signal at the amplifier output is as follows:

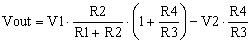(2)

If we arrange this equation differently, as in (3),

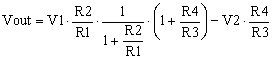(3)

one can see that, in the unique case in which

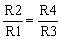(4)

the circuit amplifies the difference of the input signals, V1-V2. In other words,

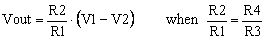(5)

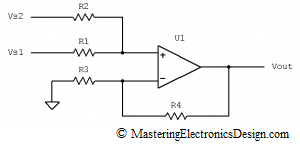
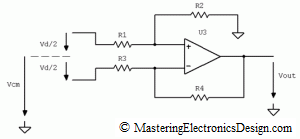
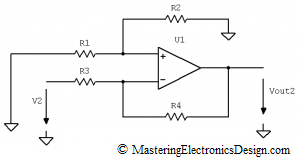
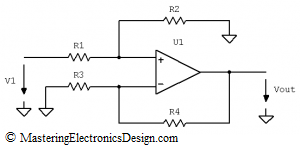
So, which is the common-mode voltage? In order to give you an answer, let’s rearrange the input signals as in Figure 2.

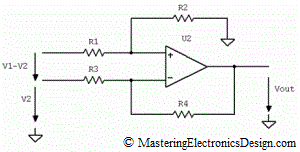
Figure 2

It should be clear now that, when the ratio of the resistor pairs is equal, V2 contribution to the output signal is zero. This can also be seen from equation (2) written differently, as in (6). In equation (6), I grouped the terms so that two main signals are shown: the difference V1-V2 and V2.

(6)

How did I arrive at this equation? It can be done in two ways: mathematically, using simple algebra methods, or, by using the Superposition Theorem.

Using the Superposition Theorem is easier, because we can consider that there are two voltage sources in the circuit in Figure 2. One source is V1-V2 and the other one is V2. Based on the Superposition Theorem if we take out one source, V2, and replace it with a wire, we find the first term of equation (6). Indeed, when R3 is connected to ground, the amplifier in Figure 2 becomes a non-inverting amplifier. As I showed in a previous article, MasteringElectronicsDesign.com: The Differential Amplifier Transfer Function, Vout1 is the voltage at the non-inverting input times the gain given by R4 and R3.

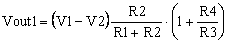(7)

With Vout1 I noted the output voltage when V2 is zero.

By rearranging

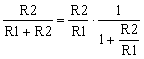we arrive at the first term of equation (6).

The second term of equation (6) is the output voltage when V1-V2 is made zero. In this case the amplifier in Figure 2 is a differential amplifier with the same voltage, V2, at both inputs. Hence, the second term of equation (6).

Equation (6) is important because it shows the common-mode error. Since the circuit amplifies the difference V1-V2, this signal appears as riding on top of V2. Hence, V2 can be seen as a common-mode voltage. If the resistor ratios are rigorously equal, the second term in equation (6) is zero. If they are not, the same term will show up at the amplifier output as an error. This is the common-mode voltage error.

How big is this error and why should the electronics designer be concerned about it?

Let’s consider that the ratio of the resistors is equal, as in equation (4), and that only R2 has a tolerance t which can be positive or negative, but smaller than 20%. In other words:

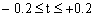(8)

For resistors, this is a practical assumption. Examples of usual resistor tolerances are 0.1%, 1%, 10%, 20%. In my example R1, R3 and R4 are ideal resistors, with 0 tolerance, while R2 has a tolerance of, say, 10% which I noted with t. This creates a mismatch in the resistor ratios R2/R1 and R4/R3 , so that the common-mode voltage V2 appears at the differential amplifier output, scaled by a factor dependent on the tolerance t. This voltage level is the common-mode error.

To calculate this error, let’s write the common-mode portion of the differential amplifier output by taking into consideration the tolerance t of resistor R2,

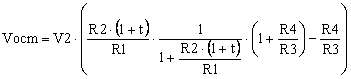(9)

where with Vocm I noted the common-mode voltage at the differential amplifier output. Since the signal of interest is the difference V1-V2, the common-mode error at the differential amplifier output is Vocm.

After calculations, and using (4), Vocm becomes

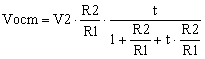(10)

We can consider that t·R2/R1 is small compared with the ratio R2/R1 which determines the gain of the amplifier. Also, for gains larger than 10, the value of 1 in the denominator can be neglected. Therefore, the common-mode error Vocm is

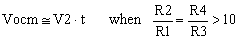(11)

Equation (10) shows that, if one resistor, R2, has a tolerance other than zero, there is a significant error at the differential amplifier output, which is approximately the common-mode voltage times that tolerance.

As an example, if V2 = 10V, V1 = 10.1V, and

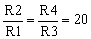
the circuit in Figure 1 amplifies the difference between these two signals, so that the output is 2V.

However, if R2 has a tolerance of +10%, the error at the circuit output is Vocm = 10V·0.1 = 1V. As a result, the differential amplifier output will be the sum of the differential output of 2V and the error of 1V, which makes 3V. The error of 1V is significant.

If R2 has a tolerance of 0.1%, the error is 10mV, which can be considered negligible in some applications. That is why the usual recommendation is to have either highly matched resistors for the differential amplifier, or resistors with 0.1% or even 0.05% tolerance.

The same logic is valid for V1 that can be viewed as the common-mode voltage, while the circuit amplifies the negative difference -(V1-V2). In the next part I will show that the convention for the common-mode voltage is

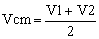
and also the reason why this is the preferred method.

How to Derive the Differential Amplifier Transfer Function

by Adrian S. Nastase

The transfer function of the differential amplifier, also known as difference amplifier, can be found in articles, websites, formula tables, but where is it coming from? Why is the differential amplifier transfer function as in the following mathematical relation?

(1)

where the resistors are those shown in Figure 1.

Figure 1

First, an important remark: This formula applies only for an ideal operational amplifier. This means that the amplifier has a large gain, so large that it can be considered infinity, and the input offset sufficiently small, so that it can be considered zero. Also, the input bias currents are sufficiently small so that they can be considered zero. I was once asked “but what is sufficiently small?” A voltage or current in electronics is considered sufficiently small, when its numerical value is 1/100 or less versus the dominant voltages or currents in the circuit. For example, if the input voltage levels, in the circuit in Figure 1, are around a few volts, and the operational amplifier input offset is millivolts or sub-millivolts, then we can neglect the input offset and consider it zero.

Having said that, do we need to know this formula by heart? Of course not. All we need to know is how to derive it. This is not difficult at all.

The transfer function can be derived with the help of the Superposition Theorem. This theorem says that the effect of all sources in a linear circuit is the algebraic sum of all of the effects of each source taken separately, in the same circuit. In other words (back at Figure 1), if we remove V1, and replace it with a short circuit to ground and calculate the output voltage, and then we do the same with V2, the output voltage of the differential amplifier is the sum of both output voltages as they were calculated with each source separately.

Let’s first remove V1. R1 cannot be left unconnected, because in the initial circuit there was current flowing through it. Therefore, let’s ground R1 (see Figure 2).

Figure 2

We can see that our amplifier becomes an inverter, which has its non-inverting input connected to ground through R1 and R2. Vout2 is given in equation (2).

(2)

Read MasteringElectronicsDesign.com: How to Derive the Inverting Amplifier Transfer Function for a proof of this function.

Now let’s remove V2 and ground R3 (see Figure 3).

Figure 3

This is a non-inverting amplifier. For an ideal operational amplifier, Vout1 is a function of V, which is the voltage referred to ground at the non-inverting input of the operational amplifier.

(3)

The resistors R1 and R2 are an attenuator for V1, so that V can be determined as in the following relation.

(4)

By replacing V in equation (3), Vout1 becomes:

(5)

Now that we have Vout1 and Vout2, and using the Superposition Theorem, Vout is the algebraic sum of Vout1 and Vout2,

(6)

which is the differential amplifier transfer function. (Q.E.D.)

Solving the Differential Amplifier – Part 3

by Adrian S. Nastase

Design a Differential Amplifier by Inspection

Designing the differential amplifier by inspection is part of the art in the analog design. Inspecting the circuit and knowing how it works, it really gives you a feeling on what the values of the resistors should be.

Looking back at the example I took in MasteringElectronicsDesign.com: Solving the Differential Amplifier – Part 1 and Part 2, we need to have an output signal of -1.25V to +2.365V with an input signal of -0.5V to 5.5V. In those two articles I used the differential amplifier transfer function and I applied math to find the resistors.

This time I am going to demonstrate how this circuit can be solved by simple reasoning and knowing how it works. Some calculations are also necessary. Cannot get rid of math totally.

Let’s write down the design requirements.

If Vin1 = -0.5V, then Vout1 = -1.25V and
If Vin2 = 5.5V, then Vout2 = 2.365V.

First, let’s remark the following: If we bring a positive signal in the V1 input, the output will swing towards the positive rail. If we connect a positive signal to V2, the output will swing towards the negative rail. Of course, if the input signal is negative, the effect is opposite (see Figure 1).

Figure 1

The transfer function of the differential amplifier is as follows:

(1)

For this function proof read MasteringElectronicsDesign.com: How to Derive the Differential Amplifier Transfer Function.

We will use V1 as the signal input, because the amplifier is not an inverter. The design requirements show that, when the input swings positive, the output goes positive as well. Let’s ignore for the moment V2. We will make V2 zero, by connecting R3 to ground (see Figure 2). If V2 is zero the transfer function can be rewritten as in the following equation.

(2)

Figure 2

The amplifier output in Figure 2 has to swing between -1.25V to +2.365V which means that the output total trip is

(3)

The same can be written about the input range

(4)

Therefore the gain has to be

(5)

In effect, this circuit is an attenuator, with a sub-unity gain.

By comparing equations (2) and (5), we conclude that

(6)

However, even if we do calculate the resistors based on equation (6), we know that there is something missing. Although the output range of 3.615V is correct for the input range of 6V, when the input is at Vin1 voltage level, the output is not at Vout1. By the same token, when Vin is at Vin2 level, the output is not Vout2. Although the total trip at the amplifier output is correct, the extremities are not in the right position. We need to introduce an offset, to move Vout1 in position, at -1.25V. If we do that, since the swing is correct, Vout2 will fall at the correct voltage level of 2.365V.

How do we calculate the offset? If we multiply Vin1 with the amplifier gain, the result is

(7)

The difference between -0.301V and Vout2 = -1.25V is -0.949V. This is the negative offset we need to introduce at the amplifier output. How do we do that? Enters V2. A positive value at V2, will move the output in the opposite direction. Comparing equations (1) and (2), the output offset is

(8)

We can choose for V2 any suitable voltage level or reference we have in our system. If this is V2 = 2.5V, and after choosing a standard value for R3 = 10 kOhm, we can calculate R4 as 3.795 kOhm. A standard value for R4 is 3.83 kOhm, with 1% tolerance.

Now that we know the resistor ratio R4/R3, R1/R2 can be easily calculated using equation (6). After calculations, R1/R2 = 1.29. Then we can choose R1 = 10 kOhm, therefore R2 = 7.754 kOhm. A standard value for R2 is 7.68 kOhm, with 1% tolerance.

>>> <<<