Apply Thevenin’s Theorem to Solve a Negative Resistance Circuit, or Current Source

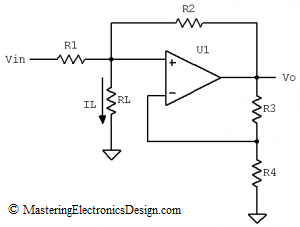
The circuit in Figure 1 is a good example of applying Thevenin’s Theorem to solve a circuit with dependent supplies. It is a negative resistance circuit and it was posted in this forum with a call for solution verification for IL as a function of Vin. With some clever resistor values, the circuit can also be a current source with RL its load. Since this fits very well with my plans to write more about Thevenin’s Theorem, I decided to post the solution here.

Figure 1

While the nodal analysis can be used, it is prone to mistakes. That is why I prefer Thevenin’s Theorem. It is an elegant solution to finding currents and voltages in networks. For complex circuits, Thevenin’s Theorem can be nested, as I showed in this article: How to Apply Thevenin’s Theorem – Part 2. Nested Thevenin Sources Method.

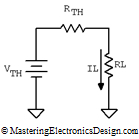
Back to our circuit. Thevenin’s Theorem says that circuits with voltage and current sources as well as resistors are electrically equivalent to one single voltage source and one resistor in series with the source. If we consider RL the Thevenin source load, the entire circuit in Figure 1 can be reduced as in Figure 2.

Figure 2

Therefore, if we calculate V_TH and R_TH, we can find IL.

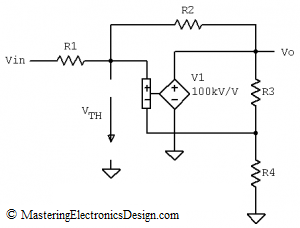
Since V_TH is the Thevenin voltage with no load, let’s eliminate RL from our circuit. Figure 3 shows the new circuit with RL eliminated. I replaced our op amp with a dependent source for convenience. If you need to know why, read this article: An Ideal Operational Amplifier Simulation Model.

Figure 3

In this simplified circuit we can apply the nodal analysis. Figure 3 shows that V_TH is

(1)

and since I2 can be written as

(2)

V_TH becomes

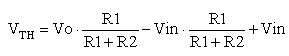(3)

I don’t like to carry large equations when solving circuits, especially when I have dimensionless ratios. So I always note a ratio of resistors like R1/(R1+R2) with a letter, say, K1.

The same circuit in Figure 3 shows that V_TH is equal with the voltage drop across R4, because the voltage between the op amp inputs is negligible. As a result, V_TH is the output voltage times the attenuation ratio R4/(R3+R4). Again, let’s note this ratio with K. So, if Vo is

(4)

replacing it in equation (3) and also replacing R1/(R1+R2) with K1, V_TH equation becomes

(5)

Solving for V_TH,

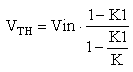(6)

The fraction that multiplies Vin is a constant and has no dimensions. Let’s note it with K2. In this case V_TH becomes:

(7)

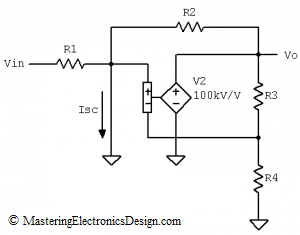
Next, let’s find R_TH. From the circuit inspection in Figure 3 one realizes that it is easier to calculate the short circuit current, at the Thevenin’s source. Figure 4 shows the short circuit and the Isc current.

Figure 4

Therefore, Isc is

(8)

And since R_TH is

(9)

by replacing Isc, R_TH becomes

(10)

And now we can calculate IL. Looking back at Figure 2, IL can be expressed as the ratio between V_TH and R_TH+RL.

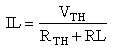(11)

After replacing R_TH in equation (11) with expression (10), and V_TH with (7) , the result is

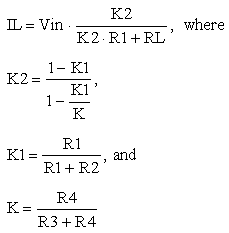(12)

>>> <<<

This result shows the circuit behavior as a negative resistance at Vin input. If the current flows into Vin, the resistance seen by Vin is negative. This happens when Vin is less than the drop on RL. The adjustments can be done with R2.

If R2 is not connected (mathematical infinity) K1 is 0 and K2 is 1, and IL becomes Vin / (R1 + RL). The current through R1 is positive, and the circuit presents a positive resistance at Vin.

Connecting R2, as R2 decreases the op amp output starts sending a current back into RL. Further decreasing R2 results in 1-K1/K to be negative and K2 becomes negative. That is the point when IL * RL is greater than Vin, the current in R1 reverses, and the circuit behaves as a negative resistance.