Derive the Transfer Function of the Common Collector Amplifier with Thevenin’s Theorem

How to Apply Thevenin’s Theorem for Solving Circuits with Dependent Sources

Besides its use to simplify and calculate currents in electrical circuits, Thevenin’s Theorem is also a great tool that we can use to derive transfer functions. This article will illustrate how to derive the small signal transfer function of the Common-Collector Amplifier with bipolar junction transistors (BJTs).

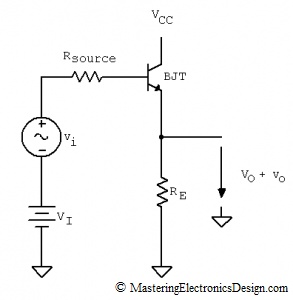
The circuit is shown in Figure 1. It is also called a repeater, so we expect that the calculated transfer function to be close to unity gain.

Figure 1

In this figure I noted with V_I the DC input bias level at the transistor input and with v_i, the AC input signal, which rides on the DC level. We need to derive the small signal transfer function v_o/v_i.

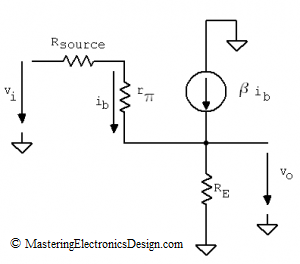
Let’s first replace the transistor with its small signal equivalent circuit (see Figure 2). This model is valid for small signals, where the transistor transfer function can be considered linear. For large signals, the model is different involving an exponential relation between its input and output signals.

Figure 2

Thevenin’s Theorem states that networks with voltage and current sources, as well as resistors are electrically equivalent to one single voltage source and one single resistor in series with the source. In order to apply Thevenin’s Theorem, let’s disconnect R_E, as in Figure 3. We will calculate the Thevenin equivalent source of this simplified circuit.

Figure 3

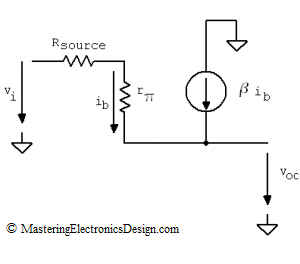
In Figure 3 I noted the open circuit voltage with voc. The derivation of this voltage is really simple. From R_source, r_&#8719 and v_oc loop, the v_oc equation is

(1)

We have one node equation in this circuit and the algebraic sum of the node currents has to be zero.

(2)

This equation can only be valid if i_b is zero. If i_b is zero, then

(3)

Next, we need the Thevenin resistance, r_th. This is the resistance seen inside the source, as looking from its output. In a previous article, How to Apply Thevenin’s Theorem – Part 1, I calculated the Thevenin resistance by short-circuiting the voltage sources and disconnecting the current sources. That method is valid for circuits with independent sources. This circuit has a dependent source, &#946 i_b, which cannot be disconnected. We need another way to calculate r_th.

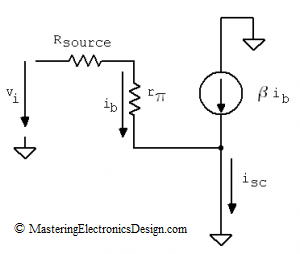
For circuits with dependent sources, r_th is calculated by dividing the open circuit voltage, v_oc, by the short circuit current, i_sc, at the circuit output. As such, let’s short-circuit the circuit output, as in Figure 4, and calculate i_sc.

Figure 4

(4)

and the Thevenin resistance is

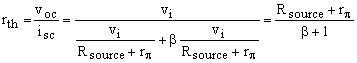(5)

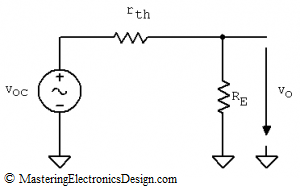
With v_oc and r_th known, we can calculate the transfer function of the circuit in Figure 1. All that’s left is to connect the emitter resistor, R_E at the Thevenin source output as in Figure 5.

Figure 5

R_E and r_th make a voltage divider for v_oc, so v_o is

(6)

Since v_oc equals v_in, the small signal transfer function of the common collector amplifier is

(7)

Q. E. D.

>>> <<<

The transfer function shows that the gain of the common-collector amplifier is almost one. Indeed, R_E (&#946+1) is large compared to R_source and r_&#8719. Mathematically speaking, when R_E (&#946+1) tends to infinity, the vo/vi limit is 1, confirming the universal knowledge that the common collector amplifier has a unity gain.