amplifier – Page 3 – Mastering Electronics Design

How to Design a Summing Amplifier Calculator

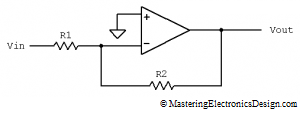
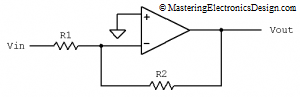
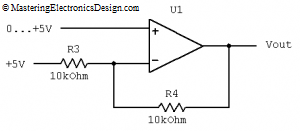
Several articles in this website describe the Summing Amplifier. In one of these articles, Solving the Summing Amplifier, I showed a numeric method to design a non-inverting summing amplifier based on its input and output voltage range requirements.

This article shows how to design a summing amplifier calculator and the mathematical relations it uses. You can find the calculator here:

JavaScript Summing Amplifier Calculator

Type the input voltage range, output range, a reference voltage and a choice of two resistors. The calculator gives you the answer for the remaining two resistors. The default values are for a bipolar to unipolar converter, which is explained in Design a Bipolar to Unipolar Converter to Drive an ADC.

What are the underlying equations?

The Virtual Ground

by Adrian S. Nastase

In my articles I talked about the op amp virtual ground and sometimes I wrote a brief explanation of this concept. In this article I will show you why an op amp input can be considered at a zero potential, without being galvanically connected to ground. Let’s take a simple circuit, the inverting amplifier.

Figure 1

In MasteringElectronicsDesign.com : How to Derive the Inverting Amplifier Transfer Function I showed the proof of its formula by using the virtual ground. The inverting input is at a zero potential, therefore virtual ground, which is a direct consequence of the feedback provided by R2 and the op amp high gain. Let’s see why.

How to Derive the Inverting Amplifier Transfer Function

by Adrian S. Nastase

Figure 1

Widely used in Analog Design, the inverting amplifier in Figure 1 has a simple transfer function.

What is the proof of this function?

Design a Differential Amplifier the Easy Way with Mathcad

by Adrian S. Nastase

For those of you who have Mathcad, designing a differential amplifier is really easy.

Let’s say you need to design a unipolar to bipolar converter and you decide to use a differential amplifier for this task. You know the input and output voltage range and you need to calculate the resistors based on a voltage reference you have in the system. All you have to do is to create a Mathcad file for a quick response. Then store it some place for future designs.

If you would like to know why the unipolar to bipolar converter can be designed with a differential amplifier, read this article, Design a Unipolar to Bipolar Converter for a Unipolar Voltage Output DAC .

Let’s take an example.

Design a Unipolar to Bipolar Converter for a Unipolar Voltage Output DAC

by Adrian S. Nastase

Unipolar to bipolar converters are useful when we have to have a unipolar component to do a certain job in a mixed signal design environment. For example, Digital to Analog Converters (DACs) may have the output voltage range 0 to 2.5 V, or 0 to 5 V, while the design asks for a range of –5 V to +5 V. To comply with this requirement, we have to design a unipolar to bipolar converter which will be inserted between the DAC output and the following bipolar stage. It looks like the circuit in Figure 1. How did I design it?

Figure 1

The Common-Collector Amplifier Input and Output Resistance – The Proof

by Adrian S. Nastase

In this article I will show a method to deduce the input and output resistance of the common collector amplifier. The common-collector amplifier is a well known circuit (see Figure 1). It is mostly used as a buffer due to its high input resistance, small output resistance and unity gain. The equations derived in this article are symbolic, as is the derivation of any other formula in this website. Still, even if the resistances’ values are not numeric, the equations are intuitive enough to show the high input, low output resistance property of the amplifier.

Figure 1

Derive the Transfer Function of the Common Collector Amplifier with Thevenin’s Theorem

by Adrian S. Nastase

How to Apply Thevenin’s Theorem for Solving Circuits with Dependent Sources

Besides its use to simplify and calculate currents in electrical circuits, Thevenin’s Theorem is also a great tool that we can use to derive transfer functions. This article will illustrate how to derive the small signal transfer function of the Common-Collector Amplifier with bipolar junction transistors (BJTs).

The circuit is shown in Figure 1. It is also called a repeater, so we expect that the calculated transfer function to be close to unity gain.

Figure 1