transfer function – Page 2 – Mastering Electronics Design

Useful Operational Amplifier Formulas and Configurations

My friends advised me that it would be helpful to have on this site the most common operational amplifier configurations and transfer functions or formulas. So, here they are. This article is not just a simple collection of circuits and formulas. It also has links to the transfer function proof for these circuits so I hope it will be very helpful. Make sure you post a comment and let me know how I can improve this page. This article will be updated, so do check it often.

Non-inverting Amplifier

Note: The proof of this transfer function can be found here: How to Derive the Non-Inverting Amplifier Transfer Function.

Voltage Follower

Note: This configuration can be considered a subset of the Non-inverting Amplifier. When Rf2 is zero and Rf1 is infinity, the Non-inverting Amplifier becomes a voltage follower. When a resistor has an infinity value, in practice it means it is disconnected.

The Transfer Function of the Non-Inverting Summing Amplifier with “N” Input Signals

by Adrian S. Nastase

In a previous article, How to Derive the Summing Amplifier Transfer Function, I deduced the formula for the non-inverting summing amplifier with two signals in its input. But what if we have 3, 4 or an n number of signals? Can we add them all with one amplifier?

Theoretically, yes. Practically, it is a different story. There is a practical limit on how many signals can be summed up with one amplifier. When the number of input signals grows, each signal component in the sum decreases in value. By the end of this article you will understand why.

Figure 1

We already saw that, for a summing amplifier with two input signals (Figure 1), the transfer function is

(1)

If we need to add 3 signals, the circuit schematic looks like the one in Figure 2. What is the transfer function of this summing amplifier with 3 inputs?

How to Derive the Summing Amplifier Transfer Function

by Adrian S. Nastase

The summing amplifier, or the non-inverting summing amplifier, is an analog processing circuit with the transfer function (the summing amplifier formula as some say) shown in the following equation.

(1)

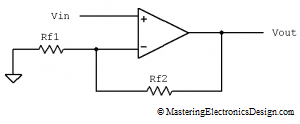
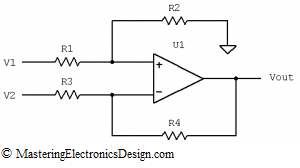
The first term of the product is the actual summing, while the second term is a gain due to the R3 and R4 resistors. I prefer this type of summing amplifier as shown in Figure 1, because it is more flexible and allows us to achieve any linear function we want.

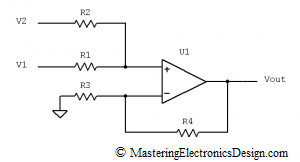
Figure 1

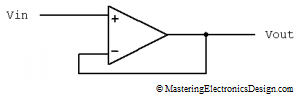
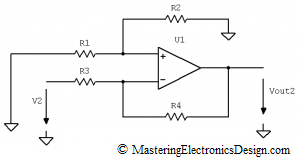
Some authors prefer the following schematic,

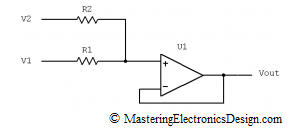
Figure 2

with the transfer function

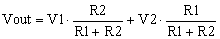(2)

One can see that the summing amplifier in Figure 2 is a subset of my preferred schematic in Figure 1. In Figure 2, R4 is zero, while R3 is infinity (open connection). It performs the analog summation between V1 and V2, with a gain of 1. Therefore, the amplifier in Figure 1 gives us more choices when designing a function with this circuit. If the gain is not needed, this should come up from calculations, as in this article Solving the Summing Amplifier.

If you followed this website, by now you probably figured that I am not a promoter of learning formulas by heart. I like to derive the transfer function if I need it. So, how do we prove this formula?

We will use the Superposition Theorem, which says that, the effect of all the sources in a circuit is equal with the sum of the effects of each source taken separately in the same circuit. Therefore, if we take out one source, V2, and replace it with a wire, we then can find the voltage in each node and the current in each branch of this circuit due to the remaining source V1. Then we do the same with V1 and then sum up the currents on each branch and the voltage levels on each node. We are only interested in Vout, so this should be simple.

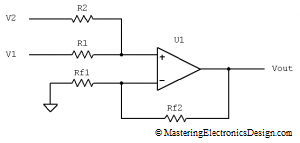
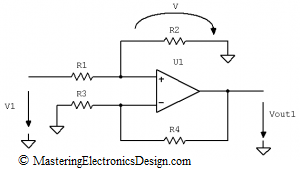
We will first make V2 = 0V, by connecting R2 to ground, as in Figure 3.

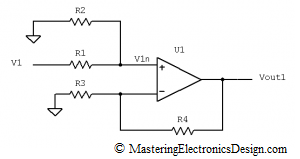
Figure 3

The Op Amp is considered an ideal component, so that the input bias currents are negligible. If the current in the non-inverting input is zero, R1 and R2 make a voltage divider for V1. The non-inverting input voltage V1n, can be written as

(3)

and, based on the non-inverting amplifier transfer function, Vout1 is

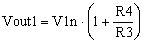(4)

By replacing V1n in (4), the output voltage is

(5)

In the second part of my demonstration, based on the Superposition Theorem, R2 is connected back to V2 and V1 = 0, by connecting R1 to ground. Following the same train of thought Vout2 can be written as

(6)

Now we have to add Vout1 to Vout2 to complete the third step of the Superposition Theorem. After factorizing the gain component 1+R4/R3, the summing amplifier transfer function becomes the mathematical relation shown in (7).

(7)

Q.E.D.

>>> <<<

This formula shows that this sum is a weighted sum between V1 and V2. This is better than a direct sum V1 plus V2, because, again, brings flexibility in design. Together with the differential amplifier, this circuit brings another treat in the art of electronics design.

The Transfer Function of an Amplifier with a Bridge in the Negative Feedback

by Adrian S. Nastase

In allaboutcircuits.com forum an interesting circuit was posted. The question was, how to determine the transfer function, Vout/Vin?

The circuit schematic was drawn as in Figure 1.

Figure 1

To make a point regarding its feedback and for clarity, I redrew it as in Figure 2.

Figure 2

Now, things started to make more sense. R1 and R2 are feedback resistors. Also, the bridge does not alter the feedback, because there is no current going through it from Vout to the bridge and to U1 input. Assuming that U1 is close to an ideal amplifier, its bias current in the inverting input is zero. Therefore, whatever current emerges from the R1 and R2 node, noted with I12, and goes to the bridge is zero. Also, the current that goes into the inverting input, In, has to be zero.

It becomes clear now that the circuit is very simple. The only currents that Vin generates are local currents, I46 and I35, through the bridge legs.

Let’s write the voltage difference V46-V35, which is the voltage that alters Vout. I will call it Vbridge.

This voltage alters Vout because it appears in the amplifier input. For that reason, Vout is given by the following equation:

(1)

The amplifier output adjusts Vout so that V35 = 0V. The inverting input is at a virtual ground, so we can write Vbridge as

(2)

If we find out V46 as a function of Vin, the circuit is solved. How do we calculate it?

By inspecting the bridge we can write V46 as follows:

(3)

The current through R3 and R5 is I35 and its value can be written as in the following equation.

With I35 known we can calculate V3.

Following the same train of thoughts, V4 is

By replacing V3 and V4 in (3), V46 in (2) and Vbridge in (1), the transfer function is

Q.E.D. (quod erat demonstrandum)

>>> <<<

This equation shows us that, if the bridge is balanced, when

the output voltage is zero. Hence, this circuit can be used for tuning, or for measurements, when one of the resistors in the bridge is a sensor. Due to the resistor ratios in the transfer function, the actual resistor value does not matter. What matters is the ratio of these resistors. As a consequence, the circuit is insensitive to temperature variations because, if all resistors are from the same technological process, the voltage at output does not change with temperature. If we choose a good operational amplifier, with a low temperature drift and low offset, this amplifier can be used in precision measurements.

How to Derive the Differential Amplifier Transfer Function

by Adrian S. Nastase

The transfer function of the differential amplifier, also known as difference amplifier, can be found in articles, websites, formula tables, but where is it coming from? Why is the differential amplifier transfer function as in the following mathematical relation?

(1)

where the resistors are those shown in Figure 1.

Figure 1

First, an important remark: This formula applies only for an ideal operational amplifier. This means that the amplifier has a large gain, so large that it can be considered infinity, and the input offset sufficiently small, so that it can be considered zero. Also, the input bias currents are sufficiently small so that they can be considered zero. I was once asked “but what is sufficiently small?” A voltage or current in electronics is considered sufficiently small, when its numerical value is 1/100 or less versus the dominant voltages or currents in the circuit. For example, if the input voltage levels, in the circuit in Figure 1, are around a few volts, and the operational amplifier input offset is millivolts or sub-millivolts, then we can neglect the input offset and consider it zero.

Having said that, do we need to know this formula by heart? Of course not. All we need to know is how to derive it. This is not difficult at all.

The transfer function can be derived with the help of the Superposition Theorem. This theorem says that the effect of all sources in a linear circuit is the algebraic sum of all of the effects of each source taken separately, in the same circuit. In other words (back at Figure 1), if we remove V1, and replace it with a short circuit to ground and calculate the output voltage, and then we do the same with V2, the output voltage of the differential amplifier is the sum of both output voltages as they were calculated with each source separately.

Let’s first remove V1. R1 cannot be left unconnected, because in the initial circuit there was current flowing through it. Therefore, let’s ground R1 (see Figure 2).

Figure 2

We can see that our amplifier becomes an inverter, which has its non-inverting input connected to ground through R1 and R2. Vout2 is given in equation (2).

(2)

Read MasteringElectronicsDesign.com: How to Derive the Inverting Amplifier Transfer Function for a proof of this function.

Now let’s remove V2 and ground R3 (see Figure 3).

Figure 3

This is a non-inverting amplifier. For an ideal operational amplifier, Vout1 is a function of V, which is the voltage referred to ground at the non-inverting input of the operational amplifier.